Epidemic, the card game
Do you know how an epidemic grows? One infects two, two infect four or three or two or one or none. All with different probabilities and a weighted average of logistic growth.
You too can be an epidemic modeller:
- Take two packs of cards. One will be used to simulate mixing, the other will track the health of the individuals
- Cut them down to the same 31 cards
- Spread one pack out face up on the table - the tracking pack
- Take the mixing pack, shuffle and deal one card - patient zero
- Take the corresponding card from the tracking pack and use it to form the first column
To form a new column, repeat the following for each card in the last dealt column:
- Remove the corresponding card from the mixing pack, shuffle and deal two cards - the two individuals met by the infected
- If they've not been dealt before remove them from the tracking pack and add to the new column
- Return all three cards to the mixing pack
Repeat until the attempt to form a new column results in a column with no cards. Herd immunity occurs when a card is dealt more than once. i.e. When the infected mix with the other infected and those that have recovered. This potentially leads to cards remaining in the spread of the tracking pack and they have no acquired immunity.
The game is an example of the minimal SIR model and averages to the standard SIR model. Both models are said to be well mixed because each individual has equal chance of meeting every other individual unlike in the social networks of real life. The letters of SIR stand for
- Susceptible to infection (the spread of tracking cards)
- Infected and infectious (the last dealt column)
- Recovered and immune to re-infection (the previously formed columns)
Changing the rules of the game so that the dealt cards are never returned to the mixing pack results in no herd immunity and thus exponential growth. In general exponential growth implies infinite resource, in a finite world one has to ask what happens and when to get a finite variable off of a curve to infinity. With these changed rules all available resources are used up and then the process comes to a halt. So if any resource is left over the growth was not exponential.
The probability that the game matches exponential growth can be calculated in a similar manner to the Birthday problem. Make a fraction by multiplying together successive fractions where the top is the number of remaining undealt cards and the bottom is the size of the pack. i.e. On the top multiply all the numbers from 31 down to 1 - this is known as the factorial of 31 (denoted 31!) and, on the bottom, 31 then repeatedly alternate between 30 and 29.
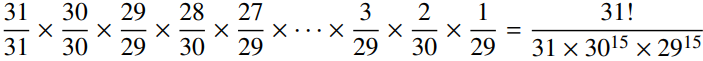
Evaluating the fraction (with specialist computer software rather than a calculator due to the size of the numbers) results in roughly a two in a million million chance. Truncating it to correspond to the first 8 cards results in roughly an even chance. Truncating it to correspond to the first 3 cards results in a certainty. i.e. The probability is equal to one.
The second and third cards being certainties correspond to the basic reproduction number (R nought) being equal to 2. It being defined as the number of individuals an infected individual would infect in an otherwise susceptible population.
When no individual recovers the result is the SI model. This can be achieved by simply dealing two cards for each card in all the columns rather than just the last column. The number of infected at any step can then be recovered by adding the height of the current column with the heights of all the previous columns. Creating a plot of those numbers results in an S shaped curve which happens to be the logistic function plus noise.
When the games of the SIR model are averaged together the resulting infection curve has one peak which occurs when logistic growth is balanced by exponential decay, that decay being due to the recovery from infection. This peak is known as the herd immunity threshold (HIT) and epidemiologists use it to calculate what percentage of a population needs to have been infected for a given R nought before an epidemic wanes away (they assume perfect mixing).