Minimal SIS model in NetLogo
NetLogo is a free environment for Agent Based Modelling. It was used to implement the Minimal SIS model:
Download the source code. Run on the web. An excerpt from the online help follows.
WHAT IS IT?
The Minimal SIS model is a discrete stochastic compartmental model of an epidemic that averages to the (ordinary differential equation) SIS model. Each individual within a population is in one of two states known, in epidemic modelling, as compartments:
- S - Susceptible to infection.
- I - Infected and infectious.
HOW IT WORKS
Setup
There are sliders to vary:
- The size of the population that will be divided into compartments.
- The basic reproduction number.
The basic reproduction number, R0, is defined as the number of individuals that will be infected by one individual in an otherwise susceptible population.
Go
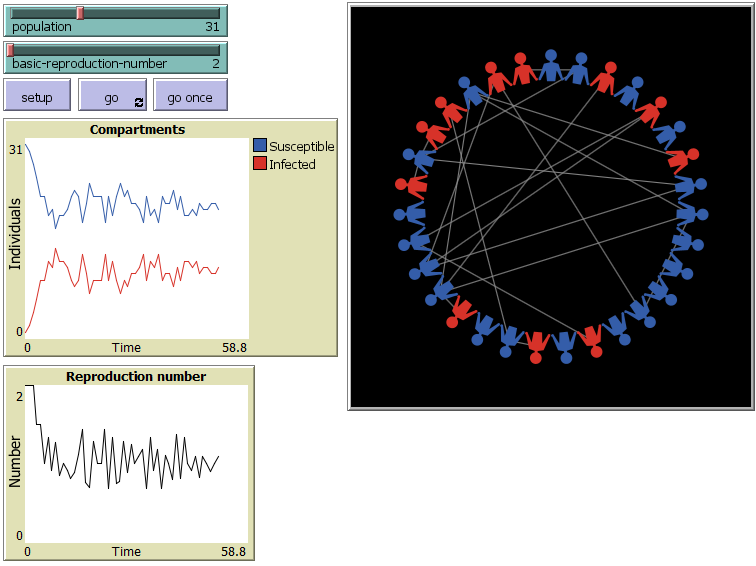
Initially one individual is infected. At each step the simulation proceeds by each infected individual selecting R0 others at random and irrespective of their state - the model is said to be "well mixed". At the end of the step the infected become susceptible and those susceptible that were selected become infected. The simulation finishes when there are no longer any infected, which is probably never.
As the simulation progresses lines are drawn between the previous generation of infected and those individuals that they were in contact with. The colour of the individuals changes according to the code:
- Susceptible - Blue.
- Infected - Red.
There are two plots of how the statistics vary as the iterations proceed. The first shows how the individuals are divided between the two compartments. The second how the reproduction number varies between zero and R0.
HOW TO USE IT
Move the sliders then press setup. Perform a simulation and note how the epidemic curves vary.
THINGS TO NOTICE
Variation of the reproduction number
If this were constant then the epidemic would be growing exponentially. The initial step plots a value of R0 which matches its definition.
If this were the SIS model instead then it would be the smooth function R0 x S / N where S is the number of susceptible and N = S + I is the size of the population.
Selecting R0 others
Each infected picking the number of susceptible is equivalent to sampling (without replacement) R0 individuals from a hypergeometric probability distribution.