Epidemiology

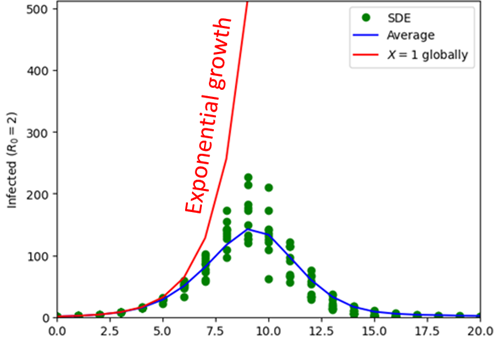
Do you know how an epidemic grows? One infects two, two infect four or three or two or one or none. All with different probabilities and a weighted average of logistic growth.

This is deducible from a discrete stochastic process that was originally conceived as a game of tag and is so simple that a simulation can be conducted with just two packs of cards. The average being logistic growth means that the process forms a derivation of the standard SIR model [1] from first principles.

The ratio of the growth to exponential growth is logit-normally distributed. As such the model debunks various stochastic models whether they have a normal distribution, use Gillespie’s algorithm or are based on the Reed-Frost model.

Being an Agent-based Model it can be easily extended. For example to a social network to show the effects of flattening the curve or of seasonality. [2]

See also:

• A NetLogo SIR simulation for running online
• A NetLogo SI simulation for running online
• A NetLogo SIS simulation for running online

[1] W. O. Kermack, A. G. McKendrick, Contributions to the mathematical theory of epidemics, part i, Proceedings of the Royal Society of Edinburgh. Section A. Mathematics 115 (1927) 700–721.

[2] Z.W.T. Mason, The minimal SIR model, validated then extended to social networks and stochastic differential equations. doi:10.31219/osf.io/y6ckv