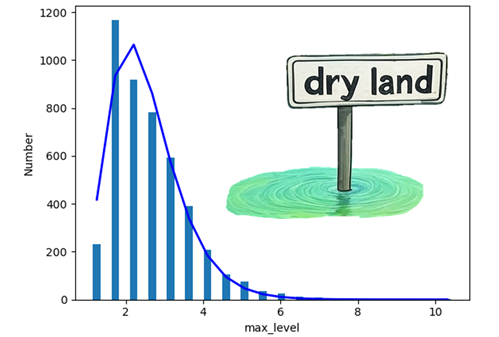
Affine growth of river heights

River heights form a skewed distribution which is variously fit by the log-normal, Gamma, Generalized Extreme Value, Weibull and Pareto distributions. In fact, it should be expected that only the one distribution should cover all the natural cases rather than the mish-mash of the existing approach.

Coin flips with offset returns are approximated by the normal distribution, linear returns by the log-normal and affine returns seem to be approximated by an appropriately scaled logit-normal distribution. A good fit for some of the river heights is performed by this latter distribution. Perhaps because, for some cases at least, affine returns result in power law tails. Further details for the flooding of the River Don at Fishlake and other cases are contained in a pre-print on GitHub.