Exponential growth?
What is exponential growth? Some variable doubles at a set rate. One, two, four, eight, sixteen, ... All the way to infinity unless it runs out of resources.
Examples are:
- Compound interest
- Grains of wheat on a chessboard - according to folklore
- Pyramid schemes
Unfortunately people see it where it isn't. This may be because its inverse function is the logarithm so that when you perform a log plot of the exponential you get a straight line. If you have a finite variable that is claimed to be growing exponentially ask what happens and when to cause that variable to leave the exponential curve. Occam's razor typically says that it was never exponential growth.
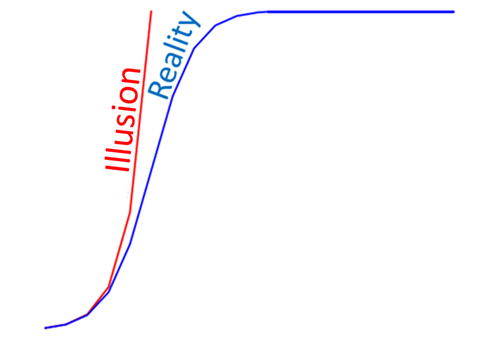
It could, for example, be on a sigmoid (S shaped) curve like the logistic instead. The logistic function is the reciprocal of one plus the reciprocal of the exponential so initially it looks like the exponential but as the exponential grows to infinity the logistic grows to one. These two curves can be seen in the picture above.
A Reductio ad Absurdum argument can also be made. For example, Charles Darwin in his seminal work On the origin of species:
Even slow-breeding man has doubled in twenty-five years, and at this rate, in a few thousand years, there would literally not be standing room for his progeny.
In 1998 the financial markets crashed harder than they could have because a lot of the financial models were based on Geometric Brownian Motion (geometric growth is an old term for exponential growth). GBM is exponential growth plus noise.
During the Covid years the media was filled with people bragging how they had failed basic Maths. Unfortunately for them the standard epidemic model from nearly 100 hundred years beforehand has logistic growth as was easily checked since lots of people were saying that the had used it to make predictions.
There are undoubtably many more examples of people extrapolating exponential growth to make unrealistic predictions.